第3章 数字和计算

古人学问无遗力，少壮工夫老始成。纸上得来终觉浅，绝知此事要躬行。

——陆游

电子计算机，从这个名称上就知道，它是用来进行计算的，只是到后来，才承担了一般的文字处理、图形处理等工作——底层仍然是计算。这或许是它的另外一个名字“电脑”日渐普及的原因吧。所以，学习编程语言，通常都是从数字和计算开始，特别是对于 Python ，它还是目前正火热的“数据科学”、“人工智能”的主流编程语言，这就更要学习如何用它计算了。本章不会探讨非常深奥的计算，所需要的数学基础仅限于初等数学，如果读者有兴趣在此基础上更上一层楼，可以参考拙作《机器学习的数学基础》（电子工业出版社，关于本书的详细内容，请参阅：http://math.itdiffer.com）。

3.1 整数和浮点数

小学数学已经学习过整数和小数——注意，数学中没有“浮点数”。现在还是要从这个基础开始，学习用 Python 语言如何表示它们。

3.1.1 整数

进入到 Python 交互模式中，输入一个整数：

>>> 3
3

就返回了所输入的数字，这说明 Python 解释器接受了所输入的那个数字，并且“认识”了它。

>>> x = 3
>>> x
3

对此也不陌生，在第2章2.3节已经自学过变量，此处的 x 即为一个变量，它引用了 3 ——这是一个对象。

上面的操作中，不论是单独输入 3 还是输入 x = 3，都是用 Python 语言创建了一个对象，它就是整数 3 。何以见得？可以用下面的方式来检验：

>>> type(3)    # (1)
<class 'int'>
>>> type(x)    # (2)
<class 'int'>

其中 type() 是 Python 的内置函数（Built-in Functions，先记住这个名词，在3.3.1节会有详细介绍），以注释（1）为例，3 作为该函数的参数，返回值 <class 'int'> 说明此对象的类型是 'int' ，即整数（integer）类型，简称“整数”。

由此可知，在 Python 中定义一个整数类型的对象非常简单，只要通过键盘输入整数即可。

如果定义 0 和负数，也是用同样的方法：

>>> zero = 0
>>> type(zero)
<class 'int'>
>>> negative_int = -9
>>> type(negative_int)
<class 'int'>

此处，之所以能如此简单地创建整数或者说整数类型的对象，完全得益于 Python 语言的开发环境已经为我们定义了名为 int 的对象类型——称为“内置对象类型”或“内置对象”，即当 Python 环境配置好之后，本地就已经存在，可以直接使用，不需要开发者来定义。

在 Python 中，与每种内置对象相对应，定义了一个同名的内置函数，通过此内置函数也可以定义该对象。以创建整数为例：

>>> a = int()
>>> a
0
>>> type(a)
<class 'int'>
>>> b = int(9)
>>> b
9
>>> type(b)
<class 'int'>

不过，如此创建整数的方式较少应用，int() 内置函数更多地应用于类型转换（参阅3.3.1节）。

在日常生活中，我们还会看到这样书写的整数：

• “005”：在整数“5”前面有两个“0”，依然表示整数“5”，那两个“0”仅仅是占位罢了；

• “6,371”：在数字中用一个英文的逗号作为分隔符（叫做“千位分隔符”，每三位数加一个逗号。这种做法比较适合于英语的语言习惯）。

但是，在 Python 中如果直接输入它们，不会如愿以偿：

>>> x = 005            
  File "<stdin>", line 1
    x = 005
          ^
SyntaxError: leading zeros in decimal integer literals are not permitted; use an 0o prefix for octal integers

Python 解释器不认识 005 ，强行输入就会出现上述异常，通过上述报错信息可知，整数不能用 0 开头 ——认真阅读报错信息，是自学者和未来的优秀开发者必备意识和能力。

>>> y = 6,371
>>> y
(6, 371)

这里没有报错，但是，所得到的对象并不是整数，是另外一类 Python 对象，详见第4章4.4节。

自学建议

如果读者对计算机的基本原理有所了解，会知道这样一个结论：在计算机上，存储的数字并非是无限大或者无限小的。例如，64 位的中央处理器所能存储的无符号整数范围是 \(0\sim 2^{64}-1\) ，如果超过此范围，就会发生算术溢出（ arithmetic overflow ）——此内容的详细解释不在本书范围，请读者自行参阅“计算机原理”的相关资料深入学习。

但是，在 Python 中如果创建超出上述理论范围的整数——注意是“整数”，不会出现溢出现象。

>>> 2**1000
10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
>>> -2**1000
-10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

2**1000 表示 \(2^{1000}\) ，显然这是一个非常非常大的整数，但是在上述计算中，没有出现溢出现象。

这是什么原因？难道 Python 神奇到能超越硬件限制吗？非也！

读者如果对这种现象感兴趣，不妨在网上搜索，能找到有关说明资料。

如果读者按照上述过程思考，并动手搜索，通过阅读有关资料对问题的缘由有所了解，就是在实践着自学中一个重要的环节：将所学内容与已有知识进行联系，并利用网络解决其中的疑问。

3.1.2 浮点数

数学中的“小数”，在 Python 中一般用“浮点数类型”表示（与浮点数对应的是“定点数”，建议读者参考3.1.1节【自学建议】的方法研究此概念），按照下面的方式，即可创建一个浮点数对象：

>>> pi = 3.14
>>> type(pi)
<class 'float'>

通过键盘输入3.14，然后用内置函数 type() 得到了此对象的类型 <class 'float'> ，即 float 类型，翻译为“浮点数”（floating-point number）类型。

3.1.1节中提到过 int 类型有与之对应的内置函数 int()，同样，float 类型也有与之对应的内置函数 float()，通过它也能够创建浮点数。

>>> f = float()
>>> f
0.0
>>> type(f)
<class 'float'>

此处用 float() 创建的浮点数是 0.0 （用变量 f 引用），它跟 0 有区别吗？类似的问题还可以是 1.0 （浮点数），与 1 （整数），有区别吗？

从纯粹数学角度看，\(0.0 = 0,\quad 1.0=1\)​ ，注意：这是数学上的比较结果，如果搬到 Python 中，会这样：

>>> 1.0 = 1
  File "<stdin>", line 1
    1.0 = 1
    ^
SyntaxError: cannot assign to literal

为什么会这样？

数学中的 \(=\) 表示两个数值相等，而 Python 语言中的 = 符号则表示的是一个变量与一个对象建立引用关系（详见第2章2.3节），如 pi = 3.14 。所以在 Python 语言中，如果判断两个值是否相等，不得不使用另外一个符号：== 。输入方法：连续输入两个英文状态下的=符号，中间不能有空格和其他符号。

>>> 0.0 == 0
True
>>> 1.0 == 1
True

返回值是 True （这是“布尔值”，参阅3.7节），说明 == 符号两侧的数字是相等的（在 == 两侧，与数字之间不论是否有空格，均不影响计算结果，但有空格更“好看”）。但是，1.0 和 1 不是同一种类型（一个是浮点数类型，另外一个是整数类型），也就是说它们不是“同一个”对象。

在 Python 语言中，要想判断“两个”对象是不是“同一个”——有点拗口的说辞，用代码来说话就容易理解了：

>>> id(1)
140696716712240
>>> id(1.0)
140696719619056

这里使用了一个内置函数 id()，它的返回值是参数对象的内存地址——形象地理解，就是对象（上述例子中是数字 1 ）在内存中的存储位置编号，并且用十进制数字的形式显示给我们。如果“两个”对象的内存地址一样，那么它们是“同一个”对象。这就如同在软件系统中，用身份证号作为注册用户的唯一标识，如果身份证号相同，就认为是同一个用户（通常假设身份证号与个人是一对一的关系）。

尽管 1.0 和 1 不是同一对象，但从数学和日常习惯的角度看，“ 1.0 就是 1”，比如财务人员填写金额的时候，通常将 \(1\) 元人民币，一般会写成 \(1.00\) 元人民币。于是乎就有一种需要，判断 1.00 这个浮点数是不是 1 ——有点绕，慢慢读，你能明白我的意思。

>>> num = 1.23
>>> num
1.23
>>> num.is_integer()   # (3)
False
>>> fee = 1.00
>>> fee
1.0
>>> fee.is_integer()    # (4)
True

在上述操作中，\(1.23\)​ 这个浮点数显然“不是” \(1\)​ 。注释（3）的含义是调用了浮点数对象 num （完整地表述，应该是“变量 num 所引用的浮点数对象”，可以简化为“浮点数对象 num ”）的 is_integer() 方法，来判断该浮点数“是不是”对应的整数，返回值是 False，说明“不是”；注释（4）的返回值是 True ，说明变量 fee 引用的浮点数 1.00 “就是”整数 1 。

请读者在阅读上文的时候注意，“是”、“不是”、“就是”等均用了引号，旨在表明其判断根据是数学中的法则，而非 Python 中根据该对象的内存地址判断是否为同一个对象。

3.2 算术运算

所谓算术运算，是指初等数学中常见的计算，如加、减、乘、除、乘方等。在数学上，每种计算都使用规定的符号实现，形式上简洁明了，Python 语言也继承了此光荣传统。表3-2-1中列出了 Python 实现算术运算所使用的运算符。

表3-2-1 算术运算符

运算符	描述	示例
+	两个对象相加	1+2=3
-	得到负数或是一个数减去另一个数	2-3=-1
*	两个数相乘或是返回一个被重复若干次的字符串	2*3=6
/	两个数相除	5/2=2.5
%	两个数相除后所得的余数	5%2=1
//	向下取整，返回两个数相除的整数	5//2=2
**	计算一个数的幂运算	5**2=25

1. 加法

对于数字而言，+ 能实现两个数字按照数学运算法则相加，例如：

>>> 2 + 3
5
>>> 2.3 + 3.1
5.4
>>> a = 4
>>> b = 6.2
>>> a + b
10.2

不论是 2 + 3 ，还是 a + b 哪种形式的运算，结果都是得到另外一个新的数字。再强调，以上均是按照数学运算法则计算的。但是，在后续的内容中会看到，运算符 + 在 Python 中的用途不局限于上述示例所演示的数学运算范围内。

到目前为止，加法运算应该没有超出所学过的数学知识范畴。

2. 减法

如果没有特别定义，运算符 - 实现的两个数字相减——这里所说的数字，目前暂且是浮点数、整数，如下操作：

>>> a = 4
>>> b = 6.2
>>> a - b
-2.2

运算符 - 的另外一个作用就是对某个数字取相反数：

>>> -4
-4
>>> -(-4)
4

这些都符合数学中的运算法则。

3. 乘法

在数学中，实现乘法的运算符是 \(\times\) ，但在编程语言中，使用的是键盘上的 * 。如果相乘的是两个数字——目前讨论的是浮点数、整数，那么与数学中的运算结果一致。

>>> 3 * 2
6
>>> 3.6 * 2.3
8.28

在表3-2-1中，对运算符 * 的描述中还有“返回一个被重复若干次的字符串”，在第4章4.2节会给予解释。

4. 除法

数学中表示两个数相除，有多种形式，比如 \(5÷2、5/2、\frac{5}{2}\)​​ 。在 Python 语言中只能选用一种符号，对于 Python 3.x ，使用 / 符号作为除法运算符，计算结果与数学中的除法运算符 ÷ 计算结果相同。

>>> 5 / 2
2.5
>>> 4.2 / 2
2.1

表3-2-1中与除法有关的符号除了 / 之外，还有 % 和 // 。

运算符 // 的含义是“向下取整”。如图3-2-1所示，对于数轴，不论它如何放置，均以其箭头所指方向——数值变大的方向——为“上”。以 \(x\)​ 轴上的点 B 为例，假设它所表示的值是 \(0 + r\)​ ，其中 \(0\le r \le 1\)​ ，比如是 \(0.7\)​ 。所谓向下取整，即取 B 点所在位置“下边”紧邻的整数，据此并结合图示可知，应该是 \(0\)​ ，可以记作 \(\lfloor0.7\rfloor=0\)​ 。再来观察 D 点，其“下”的整数是 \(-2\)​ ，若 \(D=-1.6\)​ ，则 \(\lfloor-1.6\rfloor = -2\)​ 。

图3-2-1 “向下取整”的含义

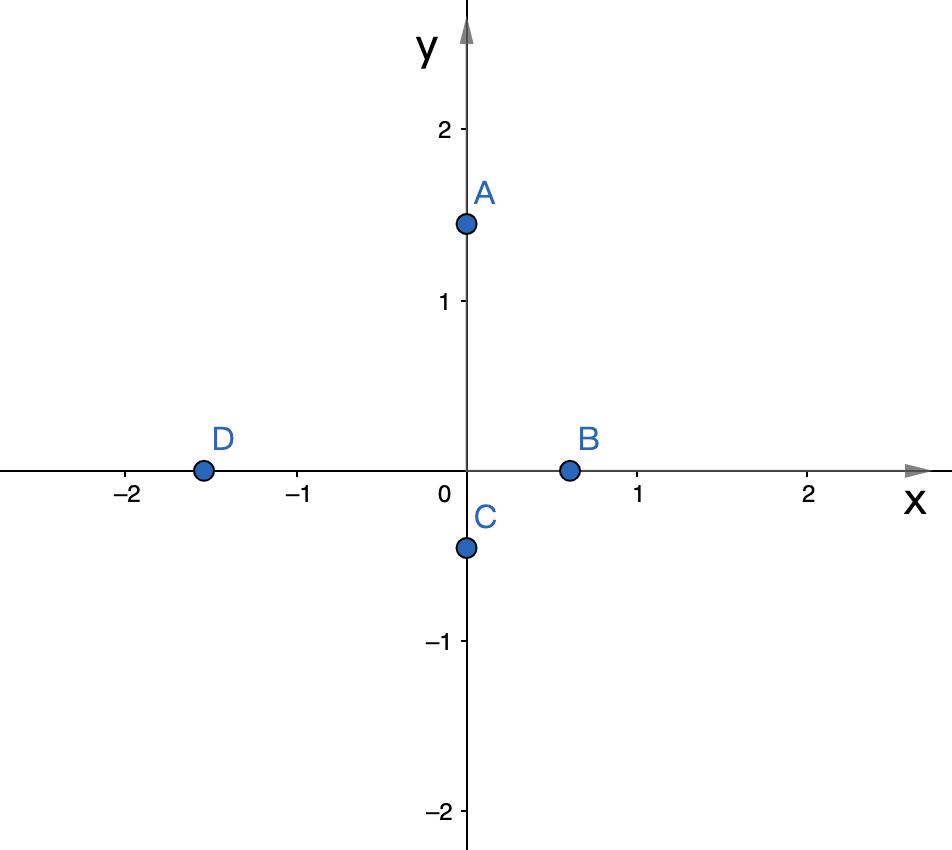
根据上述“向下取整”的解释，请读者在交互模式中执行下述操作，并结合返回值，理解 // 的含义。

>>> 5 / 2
2.5
>>> 5 // 2
2

5 / 2 的值是 2.5 ，结合图3-2-1所示的“向下取整”含义，\(2.5\) “下边”的整数是 \(2\) ，故 5 // 2 的结果是 2。

再来看负数情况：

>>> -5 / 2
-2.5
>>> -5 // 2
-3

显然 \(-2.5\) “下边”的整数是 \(-3\) ，所以 -5 // 2 的结果为 -3 。

用 // 按照“向下取整”原则得到的结果，也就是两个数字相除所得的商。

理解了 // 的计算方法之后，再理解 % 的含义——两个数相除后所得的余数。

设 \(a、d\)​ 两个数相除，以数学的形式表示为：\(a ÷ d = q\cdots r\)​ ，其中 \(q\)​ 为商，\(r\)​ 为余数，且 \(0\le |r| \le |d|\)​ 。根据数学知识可知：\(a = qd + r\)​ 。商 \(q\)​ 已经能够通过 // 得到，所以余数 \(r = a-qd\)​ 。

根据上述原理，下面通过操作，理解 % 运算符的计算结果。

>>> 5 % 2
1

根据前述计算余数的原理，在 \(5÷2\)​ 的计算中，\(q=2\)​ ，那么余数 \(r = a-qd=5-2\times2=1\)​ ，即上述返回值。再如：

>>> 7 // -9
-1
>>> 7 % -9
-2

计算 \(7÷(-9)\)​ 的余数，首先得到 \(q=-1\)​ ，根据前述计算余数的公式，\(r=7-(-1)\times(-9)=-2\)​ ，理论分析与 Python 计算结果相同。

5. 幂

在数学中，若干个数相乘可以写成该数字的几次幂，如 \(2\times2\times2\) 即为 \(2^3\) 。在 Python 中用 ** 运算符——两个乘法运算符，中间不能有空格——表示幂运算。

>>> 2 ** 3
8
>>> 2 ** -3
0.125

读者运用所学的数学知识，理解上述运算结果应不会遇到困难。

6. 科学计数法

虽然表3-2-1中没有列出科学计数法的符号——其实它不是一个运算符，但由于在科学计算中会经常用到，所以此处单独作为一项。在数学上，一个实数可以写成实数 \(a\) 与 \(10^n\) 的积： \(a\times10^n\) ，其中：

• \(n\) 必须是整数；

• \(a\)​ 是实数，通常 \(1\le|a|\le 10\)​ ，有时 \(a\)​ 也会不在此范围，届时要调整 \(n\)​ 的大小。

这种表示数字的方法称为科学计数法（Scientific Notation），由阿基米德提出。

在 Python 中，为科学计数法设计了专有表示方式：

>>> 1e10
10000000000.0
>>> 1E10
10000000000.0

上面两种表示方法，均为 \(1\times10^{10}\)​ ——其中符号 e 不区分大小写。特别要注意，这是 Python 中比较特殊的现象，在其他方面通常要求区分大小写。

E 后面如果是负整数，例如：

>>> 2.3E-4
0.00023

2.3E-4 即表示 \(2.3\times10^{-4}\) 。

任何用科学记数法表示的数，都是浮点数类型。

>>> a = 2.3E-4
>>> type(a)
<class 'float'>
>>> b = 1E1
>>> b
10.0
>>> type(b)
<class 'float'>

如果表示 \(10^8\) ，符号E前面是不是也可以省略数字 \(1\) 呢？

>>> E8
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'E8' is not defined

不行。为什么？请参考第2章2.3节关于变量的命名规则。

在一个数学算式中，如果有多个表3-2-1中的运算符，在数学称为“混合运算”。用 Python 能实现混合运算，且运算优先级与数学上的规定保持一致。

>>> 3 ** 2 + 4 / 2 - 3 + 2
10.0

在数学运算中，会用圆括号 \((\cdot)\)​​ 明确优先运算的部分，它也被引入到了 Python 语言中，而且在 Python 中还特别提倡使用圆括号，这样能提高表达式的可读性——代码的可读性强，是编程的第一原则。

>>> 3 ** 2 + 4 / 2 - (3 + 2)
6.0

需要提醒读者注意，3.1.1节【自学建议】演示了 Python 中的“大整数”不溢出现象，但是对于浮点数运算而言，若超出了中央处理器所能允许浮点数范围，会出现算术溢出。

>>> 1.9 ** 10000
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
OverflowError: (34, 'Result too large')

所以，在进行浮点数运算的时候要注意了。

但是，如果是一个用科学计数法表示的浮点数超出了系统的浮点数范围，Python 会给出另外一种处理，例如：

>>> n = 2E400
>>> n
inf
>>> type(n)
<class 'float'>
>>> 10 ** 400
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
>>> 10.0 ** 400
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
OverflowError: (34, 'Result too large')

此处的 2E400 即 \(2\times 10^{400}\) ，这个数字已经大于了宇宙中原子的总数（按照目前理论估算，在可观测宇宙中的原子总数大约是 \(10^{80}\) ），但是 Python 没有针对 2E400 出现算术溢出，而是令其值为 inf，它表示“无穷大”，并且是一个浮点数——这是 Python 的规定，请勿用数学上的规定来评判。

顺便比较 10 ** 400 与 10.0 ** 400的区别：前者返回的是整数——不会溢出，后者返回结果应该是浮点数，溢出了。

为了巩固所学，必须做个练习，当然，此练习还“另有深意”。假设两个人，一个人的质量是 \(70kg\)​​ ，另外一个人的质量是 \(50kg\)​​ ，当两人相距 \(0.5m\)​​ 的时候，他们之间的引力大小是多少？（ \(G=6.67\times10^{-11}m^3kg^{-1}s^{-2}\)​​）

显然，直接使用万有引力定理的公式 \(F=G\frac{m_1m_2}{r^2}\) 即可计算：

>>> G = 6.67E-11
>>> F = G * 70 * 50 / (0.5 ** 2)
>>> F
9.338000000000001e-07

计算表明，相距 \(0.5m\)​ 时，这两个人之间的引力大小是 \(9.3\times10^{-7}N\)​ ，仅相当于大约质量为 \(0.095\)​ 毫克的物体的重力。牛顿或许深谙此理，故终身未娶——引力仅分毫，余者又皆身外物，何必牵肠挂肚，格物穷理不孤独。

图3-2-2 艾萨克·牛顿爵士

自学建议

编程语言与数学之间有着密切的关系，本节内容仅仅是皮毛而已。如果读者有意在编程这个领域深入发展，特别建议将数学列为长期学习的内容。不是如同应付考试那样学习，而是如同刷手机那样，经常浏览一些数学内容。常见面，不陌生，用到就能想到。

《机器学习数学基础》的专题有很多数学资料，供参考。

3.3 用函数计算

算术运算符能完成的是基本运算，为了便于计算，数学上还定义了其他一些常见函数，比如三角函数、对数函数等。Python 语言中，有多种方式能够实现对常见函数计算，本节仅以内置函数和标准库中的 math 模块为例给予这方面的简要介绍，更多有关数学计算问题，请参阅《机器学习数学基础》（电子工业出版社，支持网站：http://math.itdiffer.com ），在这本书中，除了讲解有关数学知识之外，还专门说明了用 Python 语言完成数学计算的方法。

3.3.1 内置函数

在3.1.1节曾使用过内置函数 type() ，那时只是为了当时需要而引出了这个术语，未详细解释，下面对此术语进行完整地描述：Python 内置函数（Built-in Functions）是在本地计算机中配置好 Python 开发环境之后就已经可以使用的函数，不需要单独定义。在第7章会学习定义函数的方法，而内置函数是已经定义好了的，拿过来就可使用，正所谓“开箱即用”，但数量有限，表3-3-1列出了 Python 的所有内置函数。

表3-3-1 Python 内置函数

abs()	delattr()	hash()	memoryview()	set()
all()	dict()	help()	min()	setattr()
any()	dir()	hex()	next()	slice()
ascii()	divmod()	id()	object()	sorted()
bin()	enumerate()	input()	oct()	staticmethod()
bool()	eval()	int()	open()	str()
breakpoint()	exec()	isinstance()	ord()	sum()
bytearray()	filter()	issubclass()	pow()	super()
bytes()	float()	iter()	print()	tuple()
callable()	format()	len()	property()	type()
chr()	frozenset()	list()	range()	vars()
classmethod()	getattr()	locals()	repr()	zip()
compile()	globals()	map()	reversed()	__import__()
complex()	hasattr()	max()	round()

表3-3-1中的内容来自官方网站（https://docs.python.org/3/library/functions.html），图3-3-1是官方文档的截图。

图3-3-1 内置函数的官方文档

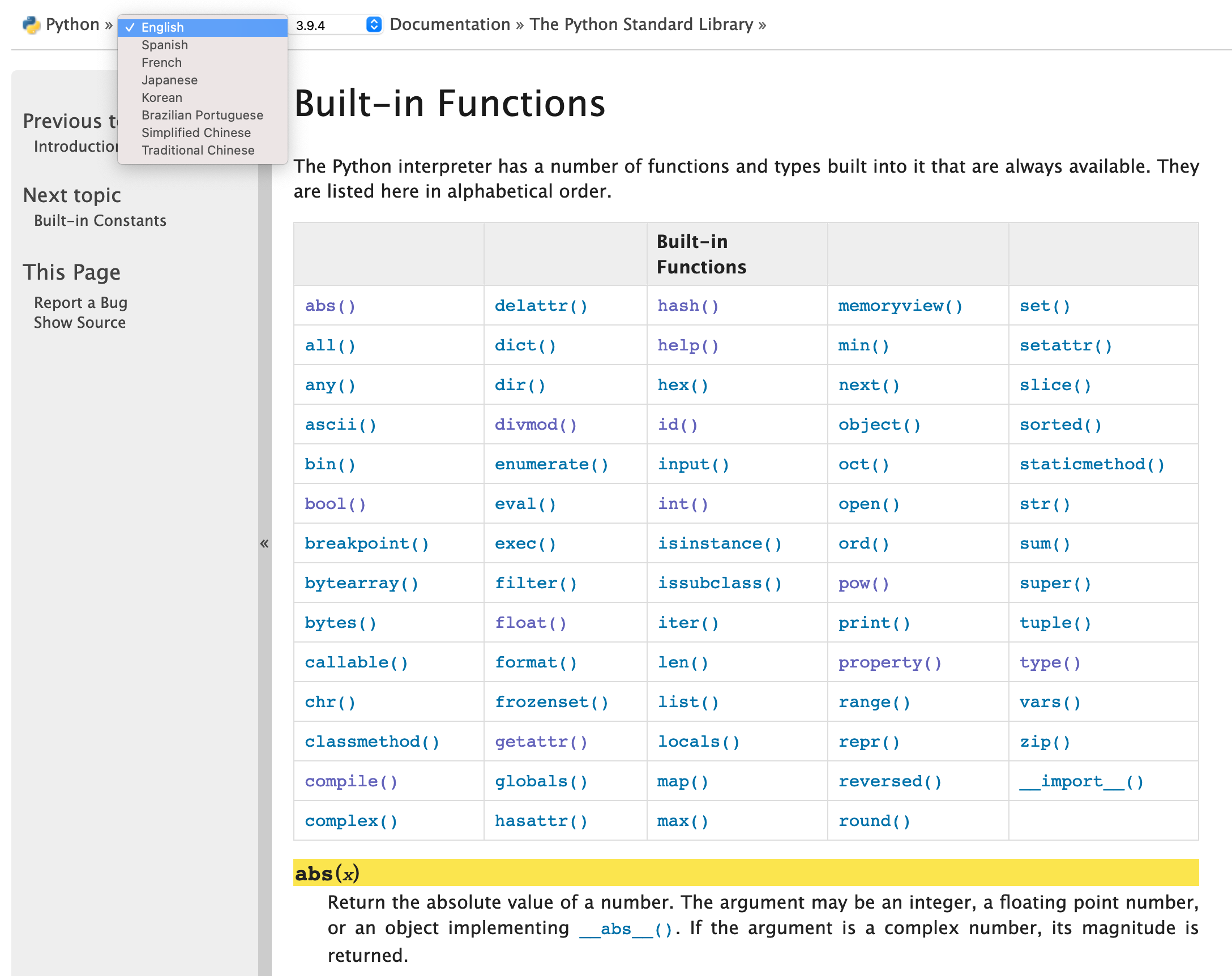
下面简要介绍其中与计算有关的几个函数，建议读者不仅仅了解这些函数的具体用法，更要从中体会自学之法。

int() 和 float()

int() 和 float() 两个内置函数与3.1节所学习过的两个内置对象类型同名，用它们能够创建相应对象或实现对象类型转化——“创建”的方法见3.1节，此处仅讨论“类型转化”。

>>> int(3.14)
3
>>> int(-3.14)
-3
>>> int(3.56)
3
>>> int(-3.56)
-3

从上述操作结果不难总结出如下结论：

• int() 可以将浮点数转化为整数；

• int() 只是截取整数部分，不是“向下取整”，也不是“四舍五入”。

看来这个函数不复杂，但“麻雀虽小五脏俱全”，解剖它就能够对所有内置函数有基本了解。请继续按照下述方式输入代码：

>>> help(int)

这里所用的 help() 也是一个内置函数，可以在表3-3-1中找到。其参数是 int 。注意，int 后面没有 () ，此时表示的是函数 int() 对象（关于“函数是对象”的话题，请参阅第7章7.3节）。

然后敲回车键，会呈现如图3-3-2所示的内容（图中是部分内容截取），按向下键或滚动鼠标，可以查看没有显示的部分。

图3-3-2 int() 的帮助文档

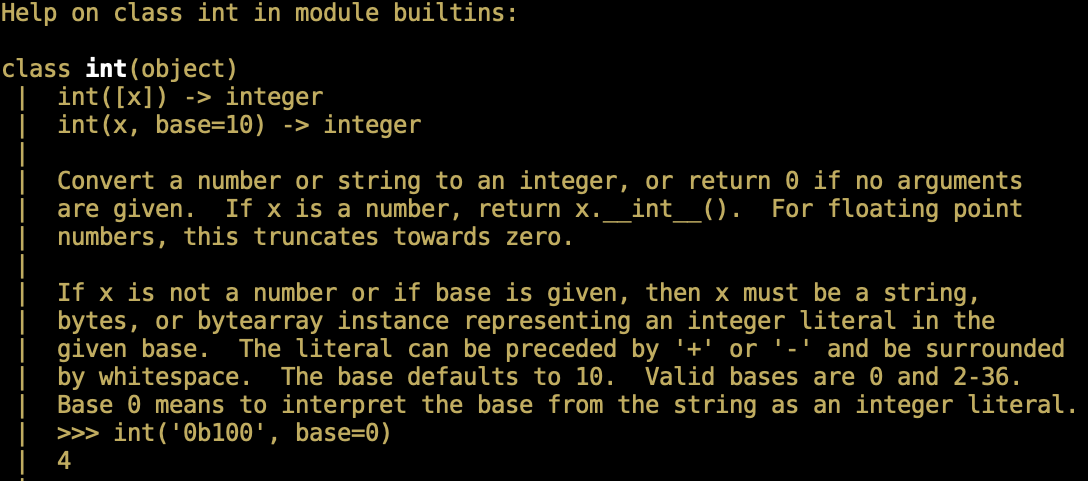
如果读者是如同上述演示那样，在终端或 CMD 窗口进入了交互模式，并用 help(int) 打开了图3-3-2所示的帮助文档，阅读完毕可以按键盘上的 q 键（英文状态下，且不区分大小写）返回到交互模式（显示 >>> 的状态）。

打开图3-3-2所示的帮助文档同时，在图3-3-1对应的 Python 官方文档的内置函数列表中，找到 int() 函数，点击该超链接，即打开网址 https://docs.python.org/3/library/functions.html#int ，可以看到如图3-3-3所示（部分截图）的内容。

图3-3-3 int() 的官方文档

比较两段文档，会发现其所言之意相同，都是对 int() 的含义和用法的解释说明。区别在于图3-3-2所示的内容，已经随着本地 Python 开发环境的配置安装到了本地（如第1章1.7.2节中的图1-7-10所示文档），可以随时查看，通常称为“帮助文档”——可以用帮助函数 help() 查看。图3-3-3所示的文档，是发布在官方网站，可以随着版本的更新随时迭代，通常称之为“官方文档”。两者本质相同。

以图3-3-2所示的帮助文档为例，解释说明其部分内容：

• int([x]) -> integer：int([x]) 表示函数 int() 的调用方法，其中参数为 [x] ，用 [ ] 符号将 x 包裹，表示该参数可以省略，即 int() （参阅3.1.1节有关操作）；-> integer 表示此函数返回值是整数。

• int(x, base=10) -> integer：这是此函数的另外一种调用方式，其中参数 x 不能省略（不再用 [ ] 符号包裹）。在 x 后面跟着英文的逗号，之后是此函数的第二个参数 base，它同样也不能省略，并且以 base=10的形式规定了默认值。关于这种调用方法，会在3.4.1节详细介绍。

• 不论是图3-3-2所示的帮助文档，还是图3-3-3所示的官方文档，均有“class int(object)”或“class int()”的形式，这里的 class 是 Python 语言中的一个关键词，关于它的有关内容请参阅第9章9.1节。

与查看 int() 函数的帮助文档的操作一样，在交互模式中输入 help(float) 即可查看 float() 函数的帮助文档，亦或在 Python 官方文档中查看该内容。建议读者认真阅读该文档，并对照如下操作理解其含义：

>>> float(3)
3.0

此处仅仅讨论了浮点数和整数对象之间的转化，在 int() 和 float() 的文档中，还指明它们也支持对字符串的转化（参阅第4章4.2节）。

divmod()

函数 divmod() 会同时返回两个数相除所得的商和余数。在交互模式中查看其帮助文档（输入 help(divmod) ），会看到如下所示的简洁描述：

divmod(x, y, /)
    Return the tuple (x//y, x%y).  Invariant: div*y + mod == x.

divmod() 的参数是两个实数 x 和 y ，返回的是 tuple类型对象（关于 tuple 请参阅第4章4.4节），其中包括两部分，第一部分是 x//y ——表示商，第二部分是 x%y ——表示余数。在文档中的式子： div*y + mod == x ，其中 div 是商，mod 是余数，这与3.2节说明 // 和 % 运算符是完全一致，请对照阅读。用以下操作熟悉这个函数的调用方法。

>>> divmod(5, 2)
(2, 1)
>>> divmod(-5, 2)
(-3, 1)
>>> divmod(7, -9)
(-1, -2)

pow()

一般情况下，函数 pow() 的作用与运算符 ** 相同，即计算某个数的幂，例如：

>>> 2 ** 3
8
>>> pow(2, 3)
8

其中 pow() 的第一个参数 2 是底数，第二个参数 3 是指数。

\(a^n\) ：其中 \(a\) 叫做底数，\(n\) 叫做指数，\(a^n\) 的结果叫做幂。

如果读者查看其文档，会发现对 pow()参数的描述方式有如下两种：

• 帮助文档中：pow(base, exp, mod=None) ；

• 官方文档中：pow(base, exp[, mod]) 。

其中的 base 和 exp 没有什么异议，重点看第三个参数： mod=None 表示此参数默认值是 None ，（ None 是一个 Python 对象，表示没有定义或者没有值）；[, mod] 表示此参数可以省略，当省略的时候与 mod=None 等效。

如果对参数 mod 赋值， 函数 pow() 与 ** 运算符就有差别了。当 mod 不为 None 时，则计算 base ** exp % mod ，并返回表达式的值（mod 为非零整数，exp大于零。建议读者通过文档理解 exp小于零时的计算过程）。

>>> 2 ** 3 % 5
3
>>> pow(2, 3, 5)
3

以上得到了 \(2^3=8\) 再除以 \(5\) ，所得到的余数。

与运算符 *** 相比，通常 pow() 函数计算性能更好。

round()

使用 round() 函数能够实现对一个实数的四舍五入——针对十进制数字而言。在交互模式中完成如下操作，并结合数学中的“四舍五入”含义理解操作结果。

>>> round(3.14, 1)
3.1
>>> round(3.56)
4
>>> round(3.56, 0)
4.0
>>> round(356, -2)
400
>>> round(356, -1)
360
>>> round(-3.56, 1)
-3.6
>>> round(-356, -1)
-360

如果读者阅读官方文档（https://docs.python.org/3/library/functions.html#round），会看到如下示例：

>>> round(2.675, 2)
2.67

根据数学知识，\(2.675\)​ 按照四舍五入原则保留两位小数，结果应为 \(2.68\)​​​ ，然而此处返回值是 2.67 。在官方文档中明确说明：“This is not a bug”，并且给出了解释（参阅3.4.2节）。

max() 和 min()

内置函数 max() 能够选出若干个数中的最大值，例如：

>>> max(3, 3.14, 7, 28)
28

注意 manx() 的参数，每个数字之间用英文的逗号 , 隔开。同理，min() 函数则返回一系列数字中的最小值。

>>> min(3, 3.14, 7, 28)
3

这两个函数，除了可以如同以上那样使用，其参数还可以是“可迭代对象”（iterable），在后续内容中，会对此给予详解。

Python 内置函数仅仅是编程中可能会用到的使用频率较高的少数几个函数，本节遴选几个，向读者演示了如何了解内置函数的使用方法。仅这几个函数还远未涵盖初等数学中常用函数，所以必须有新的工具，才能彰显 Python 在计算上的优势。

3.3.2 标准库的数学模块

Python 的发明者吉多·范罗苏姆说：Python 有“自带电池”的理念，从它的庞大软件包复杂而又可靠的能力中可见端倪（英文：Python has a “batteries included” philosophy. This is best seen through the sophisticated and robust capabilities of its larger packages. 参阅：https://en.wikipedia.org/wiki/Standard_library）。所谓“自带电池”就是指 Python 标准库（Python Standard Library，官方文档地址是 https://docs.python.org/3/library/index.html），标准库的有关程序在安装本地 Python 开发环境时已经随之安装好，与内置函数类似，也能“开箱即用”。

Python 标准库非常庞大，此处仅介绍与初等数学计算相关的模块（更多内容，参阅第11章11.3节）。

1. math 模块

标准库中的 math 模块主要提供初等数学中常用函数，官方文档地址是 https://docs.python.org/3/library/math.html。请在本地交互模式中，输入 import math ，然后敲回车键，如下所示：

>>> import math    # (1)
>>>

输入注释（1）并敲回车键后，光标停在了下一行，且没有任何返回内容——关键是没有报错，这说明本地已经正确安装了 math 模块。注释（1）的作用是将标准库中的 math 模块引入到当前环境——标准库不是内置函数，其模块都必须用关键词 import 引入之后才能使用（参阅第11章11.1节）。

接着注释（1），继续执行如下操作：

>>> dir(math)
['__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc', 'ulp']

这里使用了内置函数 dir() ，它能够返回参数对象的属性和方法——在第2章2.4节初步接触了对象的“属性”和“方法”，更详细的内容请参阅第8章。对于 dir(math) 的返回结果，也可以理解为模块 math 里面提供的函数。不妨浏览一番这些函数名称，并与记忆中的初等数学常用函数对比，是不是觉得这里已经基本涵盖了常用的函数呢？

这些函数怎么用？以余弦函数 cos 为例，根据自学经验，应该先看一看这个函数的文档：

>>> help(math.cos)

注意上述写法，不能直接写 help(cos) ，因为函数 cos 是模块 math 的一员，注释（1）引入的是这个模块，当调用其中的函数时，必须借助模块的名称（可用图3-3-4所示帮助记忆和理解。这是调用模块内的函数的一种方式，更多内容参阅第11章11.1节）。

图3-3-4 调用模块里的函数

执行上述语句，可以看到 math.cos 的帮助文档：

cos(x, /)
    Return the cosine of x (measured in radians).

由此可知，math.cos() 函数的中的参数 x 是以弧度（ \(rad\) ）为单位，并返回该值的余弦。

下面以计算 \(\cos(60^\circ)\) 为例演示 math.cos() 的使用方法：

>>> alpha = 60 / 180 * math.pi    # (2)
>>> math.cos(alpha)               # (3)
0.5000000000000001

注释（2）将以角度为单位的 \(60^\circ\) 转化为以弧度为单位的 \(\frac{1}{3}\pi\) ，但此处用浮点数表示。其中还使用了 math.pi ，其值即为：

>>> math.pi
3.141592653589793

注释（3）即为调用余弦函数，并得到了返回值——有点奇怪，暂不用管太多。

通过上述介绍，如果理解了 math 模块的使用方法，结合此前已经学得的知识，就已经能完成绝大多数初等数学中的计算了，例如计算 \(\cos\left(\frac{1}{4}\pi\right)+\lg5\times e^2\) ，且要求保留 \(2\) 位小数。读者不妨自己先试试，然后与下面的代码对照。

>>> round(math.cos(math.pi/4) + math.log10(5) * math.exp(2), 2)
5.87

2. fractions 模块

根据之前所学，如果在 Python 中表示 \(\frac{1}{3}\) ，只能用 1/3 实现，即以浮点数近似地表示。

>>> 1/3
0.3333333333333333

有没有实现精确表示的方法呢？必须得有！这就是标准库中的 fractions 模块所要解决的问题。

>>> import fractions                  # (4)
>>> a = fractions.Fraction(60, 180)   # (5)
>>> a
Fraction(1, 3)

注释（4）引入模块 fractions ，注释（5）使用 fractions.Fraction() 创建分数——注意大小写，其参数中的第一个 60 是分数的分子，第二个 180 是分数的分母，即 \(\frac{60}{180}\) 。返回值是 Fraction(1, 3) ，表示分数 \(\frac{1}{3}\) 。由此可见，注释（5）创建分数的时候，会自动化简，以最简分数作为结果。

>>> 1 / 3 + 1 / 2
0.8333333333333333

这是用浮点数形式计算 \(\frac{1}{3} + \frac{1}{2}\) 的结果，现在可以这样做：

>>> b = fractions.Fraction(1, 2)
>>> a + b
Fraction(5, 6)

如此就实现了分数的精确计算。

除了用注释（5）创建分数之外，还有其他的创建方式，此处不再赘述，请读者自行参考官方文档（https://docs.python.org/3/library/fractions.html）中的示例。下面要对注释（2）和（3）重新计算，用分数得到精确结果。

>>> alpha = fractions.Fraction('60/180') * math.pi            # (6)
>>> fractions.Fraction(math.cos(alpha)).limit_denominator()   # (7)
Fraction(1, 2)

先看结果，得到了 \(\cos\left(\frac{1}{3}\pi\right)\) 的精确值是 \(\frac{1}{2}\) 。不过，注释（6）中使用了另外一种创建分数的方法——参数形式与（5）不同（建议读者参阅官方文档示例）。注释（7）比较长，可以分为两部分，第一部分是 fractions.Fraction(math.cos(alpha)) ，这其实是第三种创建分数的方法——参数是浮点数。

>>> fractions.Fraction(0.5)
Fraction(1, 2)

如注释（3）所示，math.cos(alpha)的值是一个浮点数，再以它为参数，创建分数：

>>> fractions.Fraction(math.cos(alpha))    # (8)
Fraction(4503599627370497, 9007199254740992)

注意，math.cos(alpha) 的浮点数结果并非严格等于 0.5（如注释（3）的返回值所示），因此在注释（8）中看到所得分数只能很接近于 Fraction(1, 2) 。为此，注释（7）调用了该对象的方法 limit_denominator() ，它的作用是返回最近似的分数——需要注意此方法的默认参数 max_denominator=1000000 ，最近似的分数是以此分母计算，例如：

>>> fractions.Fraction('3.1415926535897932').limit_denominator(1000)
Fraction(355, 113)
>>> fractions.Fraction('3.1415926535897932').limit_denominator(100)
Fraction(311, 99)
>>> fractions.Fraction('3.1415926535897932').limit_denominator(10)
Fraction(22, 7)

当然，此处所创建的分数，也可以和浮点数、整数进行算术运算，或者作为函数的参数。

>>> a
Fraction(1, 3)
>>> a + 2
Fraction(7, 3)
>>> a + 0.5
0.8333333333333333
>>> a ** 2
Fraction(1, 9)
>>> pow(a, 3)
Fraction(1, 27)
>>> math.sin(a)
0.3271946967961522

问题来了，既然用分数对象能够精确计算，还要浮点数有什么用？有用！在 Python 中，运算 float 类型的对象要比运算 fractions.Fraction 类型的对象速度快，并且在一般情况下，浮点数运算的精度已经足够了。如果不是“一般情况”呢？就“鱼和熊掌不可兼得”，只能忍受“速度慢”了吗？也不是。Python 是一个开放的生态系统，除了标准库之外，还有更庞大的“第三方库”（参阅第11章），其中就有解决此问题的模块，比如 quicktions（https://github.com/scoder/quicktions）。倘若真的找不到满足需要的工具，那就是创新的机遇，一定要抓住。

针对本节内容，建议读者自己设计一些计算题进行练习——可以帮助中小学生解题。

自学建议

本节的学习中，使用了“帮助文档”和“官方文档”，这些文档是关于编程语言的最权威资料。但是，如何使用这些文档，是一个需要探讨的问题。以下是我的个人经验，供读者参考：

• 将文档当做《新华字典》那样的工具，有问题时去查询。一般地，语文学科的主要学习资料是课本，字典是必不可少的辅助学习的工具。但很少有人用《新华字典》来学习语文。有人号称“看文档就能掌握编程语言”，他一定是聪明人。

• 如果文档的原初语言是英文，尽可能看英文的文档（虽然有的文档翻译为中文了，但有的译文并没有完全表达本意）。在第1章1.6节的【自学建议】中已经就本书引用英文文档的问题给予了解释说明，这里再次强调，旨在避免读者误解。凡是有志于自学，并以成为某领域翘楚为目标者，均不会畏惧各类文档中的英文。

在本书后续内容，我会经常提醒读者查看文档，根据以往经验，会有的学习者对此破不耐烦——曾有学习者在我的课程中对这种建议给予了“狂喷”。但我不会由于他的不满而改变此风格，真正有追求的读者能理解我的建议和要求。

3.4 进制转换

前面诸节所用到的整数、浮点数、分数，均是“十进制”的数，这符合数学和日常生产生活的多数习惯。而计算机则不然，它使用的是二进制（参阅第1章1.2节）。从数学角度看，用于实现记数方式的进位制除了十进制、二进制之外，还有八进制、十六进制、六十进制等（读者也可以创建任何其他进制，比如三进制、四进制等）。同一个数字，可以用不同的进位制表示。在数学和计算机原理的资料中，会讲解如何用手工的方式实现各种进位制之间的转换——这些内容不在本书范畴，此处重点介绍使用 Python 内置函数实现进制转换，并由此观察一个貌似“ bug ”的现象。

3.4.1 转换函数

在 Python 内置函数中（如3.3节中的表3-3-1所示）提供了实现数字进制转换的函数，下面依次介绍。

1. 十进制转换为二进制

内置函数 bin() 能将十进制的整数转换为二进制，例如：

>>> bin(2)
'0b10'
>>> bin(255)
'0b11111111'
>>> bin(-3)
'-0b11'

bin() 只能对十进制的整数进行转换，所返回值是用字符串（参阅第4章4.2节）表示的二进制数字（简称“二进制字符串”），如图3-4-1所示，其中 0b 是二进制字符串前缀。

图3-4-1 返回结果组成

若将十进制的浮点数转化为二进制，是否可以用 bin()？不能！官方文档中很明确地指出：Convert an integer number to a binary string prefixed with “0b”.（https://docs.python.org/3/library/functions.html#bin）。可以试试：

>>> bin(0.1)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: 'float' object cannot be interpreted as an integer

不能使用 bin() 函数将十进制浮点数转化为二进制，但可以用别的方法实现，只不过此处暂不探讨，可以作为读者的一个思考题。

2. 十进制转换为八进制

内置函数 oct() 可以将整数转化为以 0o 为前缀的八进制字符串，如：

>>> oct(8)
'0o10'
>>> oct(256)
'0o400'

注意参数依然必须是整数。

3. 十进制转换为十六进制

内置函数 hex() 可以将整数转化为以 0x 为前缀的十六进制字符串，如：

>>> hex(16)
'0x10'
>>> hex(255)
'0xff'

十六进制的数会用数字 \(0\) 到 \(9\) 和字母 \(A\) 到 \(F\) 表示。在 hex() 返回的十六进制字符串中，所用的 \(A\) 到 \(F\) 的字母均为小写。

对于十进制的浮点数，虽然不能用于 hex() ，但浮点数对象有一个方法可以实现向十六进制的转换。

>>> float.hex(0.1)
'0x1.999999999999ap-4'
>>> 0.1.hex()
'0x1.999999999999ap-4'

其实，这里得到的十六进制字符串与十进制浮点数 0.1 并非严格相等（参考3.4.2节）。

4. 二进制转换为十进制

如果在交互模式中直接输入二进制数，比如 01，Python 解释器并不接受——所接受的是十进制数。

>>> 01
  File "<stdin>", line 1
    01
     ^
SyntaxError: leading zeros in decimal integer literals are not permitted; use an 0o prefix for octal integers

当然，有的读者可能输入的是 11 ，不会报错，但 Python 把它看做二进制 11 了吗？没有！它显然被 Python 认定为十进制的整数了。

>>> 11
11
>>> type(11)
<class 'int'>

但是，如果在交互模式中这样输入二进制数字：

>>> 0b11
3
>>> 0b10
2
>>> 0b11111111
255

注意，输入的不是“二进制字符串”，而是在二进制数前面写上了前缀 0b，表示当前所输入的是二进制数，返回值则是对应的十进制整数。这种方式仅限于交互模式，在程序文件中不能这样做——千万不要将 >>> 0b11 复制到 .py 文件中。

更常用的方法是使用内置函数 int() ，在3.3.1节中提到过， int(x, base=10) -> integer 会在本节介绍，就是这里：

>>> int('0b10', 2)
2
>>> int('11111111', 2)
255

其中的'0b10' 和 '11111111' 都是二进制字符串，并且要设置参数 base=2 ，即说明参数中的数字是二进制数字——不明确“告诉” Python ，它不知道 '0b10' 和 '11111111' 表示的是二进制字符串。

同样用 int() 函数，也能表示八进制、十六进制的整数，并返回所对应的十进制整数。

>>> int('0xff', base=16)
255
>>> int('0o10', base=8)
8

3.4.2 不是 bug

在3.3.1节介绍内置函数 round() 时引用了官方文档的一个示例：

>>> round(2.675, 2)
2.67

该文档中明确说明：“This is not a bug”。那是什么呢？

类似的现象，其实还有，比如：

>>> 0.1 + 0.2
0.30000000000000004
>>> 0.1 + 0.1 + 0.1 - 0.3
5.551115123125783e-17
>>> 0.1 + 0.1 + 0.1 - 0.2
0.10000000000000003

这些计算中都有一些“误差”，也不是 Python 的 bug。

由于计算机是执行二进制计算的，要完成十进制数字的计算，不得不将十进制数字转化为二进制。对于十进制的整数而言，都有精确的二进制数对应。但是，对于浮点数就不总有精确的二进制数对应了。

例如，\(0.1\) 转化为二进制是：\(0.0001100110011001100110011001100110011001100110011...\) 。这个二进制数不精确等于十进制数 \(0.1\) 。同时，计算机存储的位数是有限制的，所以，就出现了上述“误差”。

这种问题不仅在 Python 中会遇到，在所有支持浮点数运算的编程语言中都会遇到，所以它不是 Python 的 bug 。

明白了原因后，该怎么解决呢？就 Python 的浮点数运算而言，大多数计算机每次计算误差不超过 \(\frac{1}{2^{53}}\) 。对于大多数任务来说，通过“四舍五入”（round() 函数，参阅3.3.1节）即能得到期望的结果。

但是，如果遇到“较真”的要求，怎么办？

>>> import decimal
>>> a = decimal.Decimal('0.1')
>>> b = decimal.Decimal('0.2')
>>> a + b
Decimal('0.3')
>>> float(a + b)
0.3

decimal 是 Python 标准库的一个模块，官方地址是 https://docs.python.org/3/library/decimal.html 。如上述代码示例，分别创建了与浮点数 \(0.1\) 和 \(0.2\) 对应的两个对象（ decimal.Decimal 类型），它们之间相加，所得结果即为准确的 \(0.3\)​ 。但是这样计算的速度要低于浮点数运算。

decimal 模块不仅能解决上述计算“误差”问题，还有很多用途，比如某个业务要求所有计算结果必须有 \(3\)​​ 位有效数字（注意与“四舍五入”不同），可以这样实现：

>>> from decimal import Decimal, getcontext
>>> getcontext().prec = 3
>>> Decimal(1) / Decimal(7)
Decimal('0.143')
>>> Decimal(3) * Decimal(math.pi) ** 2
Decimal('29.6')

此外，decimal.Decimal 对象亦有支持常见计算的方法。建议读者在学习完第8章和第9章，再认真阅读此模块的官方文档，并练习使用其中的各个方法。

自学建议

编程语言是基于计算机基本原理而存在的，因此，建议读者在学习本书之余——学有余力，阅读有关计算机基本原理的书籍，这样不仅对编程语言，乃至于以后的工作实际都会大有裨益。例如对于本节提到的“进制转换带来的计算误差”问题，要想“知其所以然”，就不得不求助于计算机基本原理的知识。

我在本网站和微信公众号【老齐教室】都会发布有关计算机原理的内容，读者可查阅参考。

3.5 复数

数学中的复数是用虚数单位 \(\rm{i}\) 创建的一类数，其中 \(\rm{i}^2=-1\) ，通常的形式为 \(a + b\rm{i}\) 。在 Python 中也能定义复数，但表示虚数单位的字母与数学中的习惯有别。

>>> c = 3 + 4j    # (1)
>>> type(c)
<class 'complex'>

按照复数的数学形式，使用注释（1）创建了 Python 中的复数（ Complex ），注意，其中 4j 并不是表示 4 * j 。Python 中的复数与前面所学习的浮点数、整数都是一种对象类型。

如果创建只有一个虚数单位的复数，即数学上的 \(\text{i}\) ，不能这样做（这是什么原因？读者是否能根据已经学过的知识给予解答）：

>>> j
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
NameError: name 'j' is not defined

必须要写上虚数单位前面的系数，即：

>>> 1j
1j
>>> type(1j)
<class 'complex'>

此外，在 Python 内置函数中有与类型同名的 complex() 函数，可以用来创建复数对象。

>>> complex(3, 4)
(3+4j)
>>> complex(0, 0)
0j

在数学上，复数、浮点数、整数，能够依据算术运算的法则进行运算，在 Python 中也一样。

>>> a = complex(2, 5)
>>> a
(2+5j)
>>> (a + 3.4) * 2
(10.8+10j)
>>> a / 3
(0.6666666666666666+1.6666666666666667j)
>>> a ** 2
(-21+20j)
>>> pow(a, 2)
(-21+20j)

上面的演示中，内置函数 pow() 的参数可以是复数，但不是所有的内置函数都接受复数，请读者特别注意其文档中的说明。在3.3.2节所学习过的 math 模块的函数，都不支持复数。若要对复数使用初等函数，可以用另外一个名为 cmath 的模块（官方文档：https://docs.python.org/3/library/cmath.html ）。

>>> import cmath
>>> dir(cmath)
['__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atanh', 'cos', 'cosh', 'e', 'exp', 'inf', 'infj', 'isclose', 'isfinite', 'isinf', 'isnan', 'log', 'log10', 'nan', 'nanj', 'phase', 'pi', 'polar', 'rect', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau']

用 dir() 函数列出了 cmath 中的函数和常数名称，这里的函数接受整数、浮点数、复数作为其参数。

>>> cmath.sin(a)
(67.47891523845588-30.879431343588244j)
>>> cmath.sin(1)
(0.8414709848078965+0j)

还可以通过复数对象的 conjugate 方法和 imag, real 属性，分别得到相应的共轭、虚部和实部：

>>> a.imag    # 虚部
5.0
>>> a.real    # 实部
2.0
>>> a.conjugate()    # 共轭
(2-5j)

最后，留个读者思考一个小问题：

>>> abs(-7)
7
>>> abs(3.14)
3.14
>>> abs(3 + 4j)
5.0
>>> abs(3 - 4j)
5.0

内置函数 abs() 的参数如果是浮点数或整数，则返回其绝对值；如果是复数，返回值是什么含义？

3.6 比较

数学中的“比较”是很单纯的，就是衡量两个数字哪个大、哪个小。但是 Python 语言中，除了兼顾数学上的“比较”之外，还把事情搞得复杂了一些，且看本节揭示其复杂性。

3.6.1 比较运算符

3.2节学了算术运算符，除此之外，数学中还有“比较运算符”，在 Python 中如何实现？也很直接，请读者观察键盘（如图3-6-1所示），其中有输入比较运算符的键，按下“ Shift ”键，然后按下标有“ < ”或“ > ”的键，即可输入小于号或大于号——要在英文状态。

图3-6-1 比较运算符的键

比如，在 Python 交互模式中输入：

>>> 3.14 < 2.72   # (1)
False
>>> 3.14 > 2.72   # (2)
True

注释（1）和（2）是比较表达式，即两个数字对象进行比较的不等式。如果不等式成立，就返回True ，否则返回 False 。

除了注释（1）（2）表达式中的小于号和大于号之外，其他比较运算符列在表3-6-1中，请读者参考。

表3-6-1 比较运算符

运算符	描述	实例 （设 a=10，b=20）
==	等于，比较对象是否相等	(a == b) 返回 False
!=	不等于，比较两个对象是否不相等	(a != b) 返回 True
>	大于，返回 a 是否大于 b	(a > b) 返回 False
<	小于，返回 a 是否小于 b	(a < b) 返回 True
>=	大于等于，返回 a 是否大于等于 b	(a >= b) 返回 False
<=	小于等于，返回 a 是否小于等于 b	(a <= b) 返回 True
is	判断对象的同一性	(a is b) 返回 False
Is not	对象同一性判断的否定	(a is not b) 返回 True

表3-6-1中所列的各项比较运算符，不仅能够用于比较数字，还能应用于后续的其他对象类型的比较——这就是 Python 中“比较”的一种复杂性体现。

3.6.2 相等和同一

表3-6-1中显示的“ == ”符号，是用来比较两个对象是否相等，请注意区别于数学中习惯的“ = ”符号。在高级编程语言，“ = ”用于赋值语句（参阅第6章6.1.1节）。

>>> a = 9    # 赋值语句，变量和对象建立引用关系
>>> b = 9.0
>>> a == b   
True

a == b 即比较变量 a 引用的对象与变量 b 引用的对象是否相等。

在3.1.2节业已学习到了 == 的含义，并且同时提到了“相等”并不意味着是“同一个对象”，如上述示例中的整数 9 和浮点数 9.0 。下面再通过演示，深入理解“相等”和“同一”的区别。

如3.1.2节所述，在 Python 中两个对象是否“同一”，可以看它们的内存地址是否相同，比如：

>>> a = 256
>>> b = 256
>>> id(a) == id(b)    # (3)
True

内置函数 id() 返回了参数对象的内存地址，注释（3）的表达式返回了 Ture ，说明 a 和 b 引用的对象内存地址相同——这就是重复3.1.2节的内容，读者不要急躁，看下面的：

>>> c = 257
>>> d = 257
>>> id(c) == id(d)
False
>>> id(c)
140374295342960
>>> id(d)
140374295340752

是不是很神奇？同样是整数，这时候两个变量分别引用了两个不同的对象。

如果查看浮点数——所有浮点数都如此。例如：

>>> f = 3.14
>>> g = 3.14
>>> id(f)
140374295339504
>>> id(g)
140374295339312

变量 f 引用了浮点数对象 3.14 ，Python 在内存中创建了该对象；变量 g 再引用一个浮点数对象，只不过此对象的值还是 3.14，Python 在内存中又创建了一个新对象，而没有将变量 g 指向前面那个 3.14 对象。前面看到的变量 c 和 d 也如此，分别引用两个不同的 257 对象。但是变量 a 和 b 则不然，虽然操作与后面的二者类似，但它们引用了同一个 256 对象。

这是因为 Python 中做了一个规定，将常用的值（整数 -5 到 256）默认保存在内存中，从而节省内存开支。如果变量引用这些值，就直接指向内存中已有的，不再新建。所以，才出现上面的操作结果。

判断两个对象是否相等，使用 == 符号。虽然注释（3）的表达式也能判断两个对象是否“同一”，但显得不那么“近乎自然”——编程语言的发展方向就是越来越趋近自然语言。于是，Python 提供了一个用于判断对象是否“同一”的关键词 is 。

>>> c is d
False
>>> a is b
True

is 用于判断两侧的对象是否是同一个，返回 False，说明不是同一个对象，否则返回 True 。因此 is 也被称为身份运算符。

自学建议

“内存”，全称“内部存储器”。计算机的存储系统可以分为两大类：内部存储器和外部存储器。其中内部存储器接受 CPU 的控制与管理，只能暂存数据信息。

此外，“内存”这个词在某些语境下，还是“主板上的RAM”的代称。

请读者查阅有关资料，了解存储器知识。

“相等”和“同一”的上述探讨，不仅仅存在于数字对象，后续要学习的其他类型的对象，也有同样问题，请读者届时要特别注意辨识 is、== 的作用效果。

3.7 逻辑运算符

对 True 和 False 应该不陌生了，前面已屡次出现，但是我们还没有对这两个对象深入探讨过，在交互模式中可以检验它们的类型：

>>> type(True)
<class 'bool'>
>>> type(False)
<class 'bool'>

由返回结果可知，这两个对象属于 bool 类型，翻译为“布尔”类型。布尔类型的对象只有两个：True 和 False，也称为“布尔值”（Boolean value）。

在学习布尔型对象的有关知识之前，必须了解与此相关的一名数学家：乔治·布尔（George Boole）——“布尔”类型即以这位数学家的姓氏命名。

图3-7-1 乔治·布尔

乔治·布尔出生于英格兰，父亲是一名鞋匠。布尔接受过小学教育，此后由于家境贫寒，不能在正规的教育系统中学习，只能依靠自学——注意是“自学”。16岁时谋得一个初级教学的职位（junior teaching position） ，由此开启了他的教育教学和学术生涯。在教学中，布尔对当时的数学课本不满意，就开始研读数学家的论文，并且在变分法方面有了新的发现——是我辈后生的榜样。

1847年，出版了《The Mathematical Analysis of Logic》；1854年，出版了著名的《The Laws of Thought》，这本书中介绍了现在以他的名字命名的布尔代数。由于布尔在符号逻辑运算中的特殊贡献，编程语言中逻辑运算也称为布尔运算，将其结果称为布尔值。

Python 中有与 bool 类型同名的 bool() 内置函数，以某个对象作为它的参数，可以得知“真、假”，即返回布尔值 True 或 False 。

>>> bool(0)
False
>>> bool(1)
True
>>> bool(-1)
True

对于数字而言，0 为“假”，非零为“真”。在 Python 中，还有其他对象是“假”（有的对象还没有学到，在后续内容会介绍），列举如下：

• None 和 False；

• 0，0.0，Decimal(0)，Fraction(0, 1)；

• 空序列和集合：'', (), [], {}, set(), range(0) 。

在 Python 中，还有如此结果：

>>> True == 1
True
>>> False == 0
True

两个布尔值分别与两个整数对应相等，所以：

>>> True + False
1
>>> 2 + True
3
>>> 3 * False
0
>>> True / False
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ZeroDivisionError: division by zero

当然，通常我们不会用 True 和 False 直接替代算术运算中的 1 和 0 。

实现布尔值之间的运算，称为逻辑运算，其中的运算符号叫做逻辑运算符。Python 中的逻辑运算符有 and、or 、not 三个。

(1) and

and ，翻译为“与”运算，其运算过程如图3-7-2所示——特别注意，可能与读者在数学中所学不同，也可能与某些其他资料中的讲述不同，但这是 Python 中逻辑运算的真实过程。

图3-7-2 and 运算

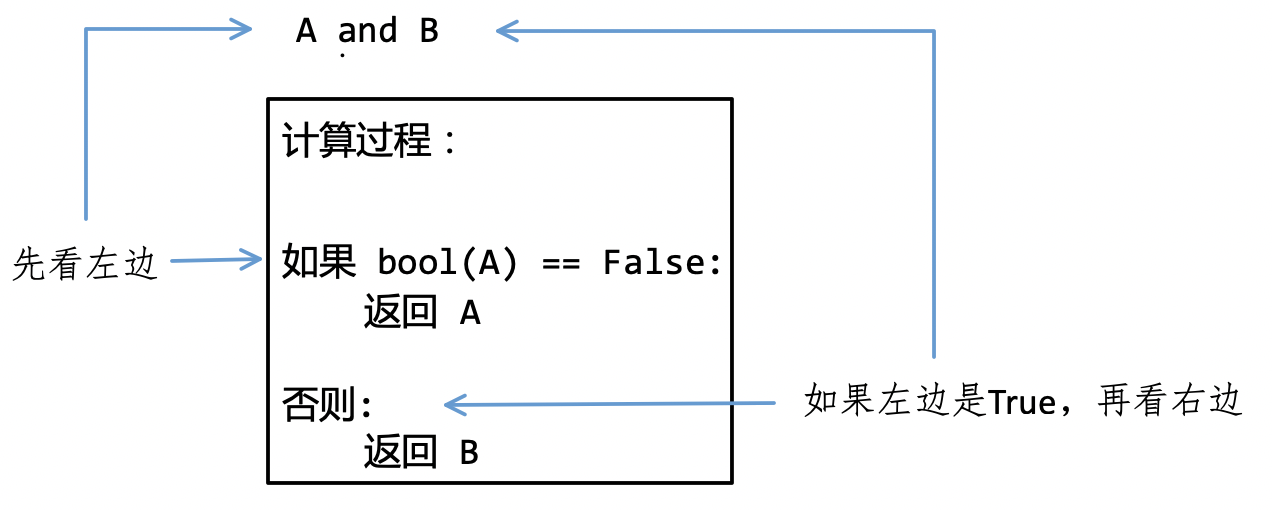
例如：

>>> 0 and 1    # (1)
0

依照图3-7-2所示的过程，注释（1）的计算过程如下：

1. 计算 bool(0) ，其值为 False ；

2. 显然 bool(0) == False 成立，即此式的值是 True；

3. 于是返回 0 。

在此计算过程中，没有计算 bool(1) 即得到了返回值，将此计算过程形象地称为“短路计算”，显然，短路计算节省了计算资源。

>>> 2 and 1    # (2)
1

对于注释（2），因为 bool(2) 的返回值是 True，即 bool(2) == False 不成立，按照图3-7-2所示的过程，则返回 1 ——不需要计算 bool(1) ，而是直接返回 and 右边的对象。

请务必理解上述运算过程。虽然有的资料中坚持要看 and 的两侧的对象的布尔值，并且与图3-7-2所示的过程得到同样的结果，但所耗费的“能源”不同，“节能减排”已是共识，Python 也不例外。

再看如下运算：

>>> 4 < 3 and 4 < 9   # (3)
False

并没有返回 4 < 3 ，而是返回了 False 。不妨还用图3-7-2所示的运算过程理解注释（3）：

1. 计算 bool(4 < 3) ，其值为 False；

2. bool(4 < 3) == False 成立；

3. 返回 4 < 3 ，注意这是一个比较运算表达式，Python 会计算它的结果 False；

4. 最终得到了注释（3）的返回值 False 。

(2) or

or，翻译为“或”运算。其运算过程如图3-7-3所示：

图3-7-3 or 运算

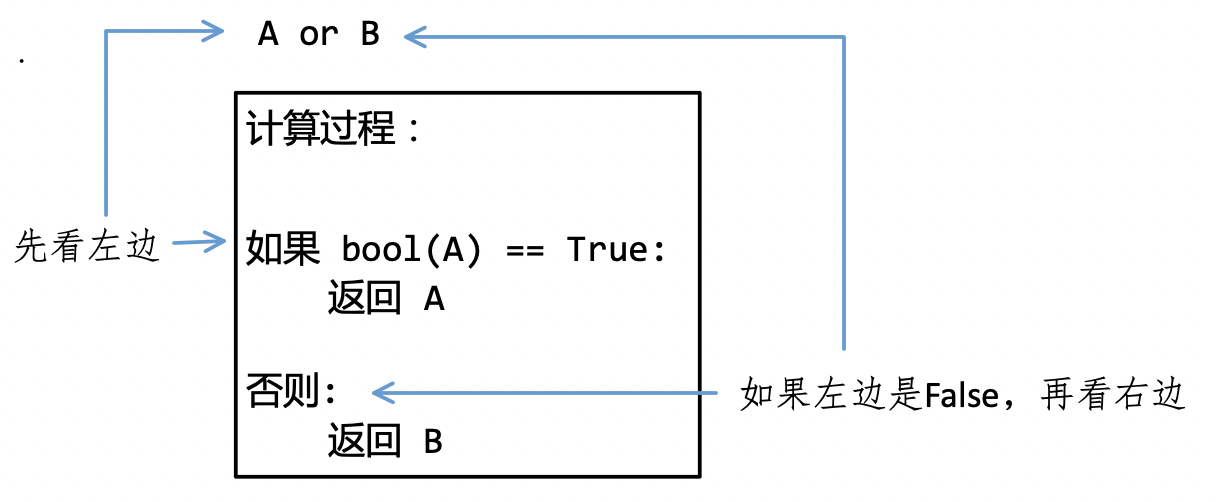
根据对 and 的自学经验，再学习 or 就顺风顺水了。首先观察图3-7-3所示的运算过程，再按照如下所示在交互模式中操作，并请读者自行解释运算过程（仿照 and 中的解释）。

>>> 0 or 1
1
>>> 1 or 2
1
>>> 4 > 3 or 4 > 9
True

(3) not

not ，翻译成“非”，返回对象的布尔值的相反值，如：

>>> not(2)    # 或写成 not 2
False
>>> not(0)
True
>>> not(4 < 3)
True

对于整数 2 ，bool(2) 的值为 True ，其相反值为 False ；对于 0 ，bool(0) 的值为 False ，其相反值为 True ；对于 4 < 3 ，bool(4 < 3) 的值为 False ，其相反值为 True 。

在3.6.1节的表3-6-1中有一个运算符 is not ，用它可以判断两个对象的“不同一性”：

>>> a = 257
>>> b = 257
>>> a is b
False
>>> a is not b    # (4)
True

提醒注意，注释（4）中的 not 不是逻辑运算符，是 is not 的组成部分。

如果在一个表达式中出现了以上三个逻辑运算符中的两个或更多，那么它们之间就有运算优先级的问题了，表3-7-1按照从高到低列出了这三个逻辑运算符的优先级。

表3-7-1 逻辑运算的优先级（从高到低）

顺 序	符 号
1	not x
2	x and y
3	x or y

例如：

>>> not 2 and 1
False
>>> 2 and not 0
True

第一个表达式中，先计算 not 2 ，返回值是 False ；再计算 False and 1 ，返回值为 False 。第二个表达式请读者自行解释。

从可读性和准确性的角度看，在复杂的表达式中，最好使用括号——用括号指定计算单元，意义非常明确，不易出错。

>>> 4 > 3 and (3 > 9 or 5 < 6)
True
>>> not(True and True)
False

在某些故意刁难人的考试中，有可能让你判断 0 < 0 == 0 的结果——不让用计算机调试，在空白处写出答案。

如果把这个式子写入到 Python 交互模式中：

>>> 0 < 0 == 0   # (5)
False

你猜对了吗？

先做一个郑重声明，我不推荐使用类似注释（5）那样的写法。

注释（5）本质上是：

>>> (0 < 0) and (0 == 0)    # (6)
False

我认为写代码不是炫酷。

至此我们学习了算术运算、比较运算和逻辑运算，此外，还有位运算及其运算符，但是，本书不打算对此内容给予介绍，有兴趣的读者可以自行查阅有关资料。

自学建议

从本章开始，代码量明显增加了。如果你觉得这么多内容记不住而略有焦虑或者担心自己学会不会，大可不必。因为编程是一个实践性非常强的工作，通过大量的实践后，常用的东西自然就熟练，不常用的也知道怎么查找了。所以，关键在于“实践”。学习过程的“实践”，首先将学习过的内容反复练习，而不是因为觉得“很简单”就不练习。“看看似乎明白，敲敲常出错误”，可以说编程技能是“练”出来的，不是“教”、“看”出来的。